C Program For Gauss Elimination Method With Pivoting
Gaussian Elimination Next: Up: Previous: To solve, we reduce it to an equivalent system, in which U is upper triangular. This system can be easily solved by a process of backward substitution. Denote the original linear system by, where and n is the order of the system. We reduce the system to the triangular form by adding multiples of one equation to another equation, eliminating some unknown from the second equation. Additional row operations are used in the modifications given later.
We define the algorithm in the following: Gaussian Elimination Algorithm: Step 1: Assume Define the row multipliers. It is easy to see that A=L U. Also det(A)=det(U)=-1 Pivoting and Scaling in Gaussian Elimination At each stage of the elimination process given above, we assumed the appropriate pivot element. To remove this assumption, begin each step of the elimination process by switching rows to put a non zero element in the pivot position. If none such exists, then the matrix must be singular, contrary to assumption. It is not enough, however, to just ask that pivot element be nonzero.
Gauss Elimination Method Algorithm and Flowchart. It is straightforward to program, and partial pivoting can be used to control rounding errors. 9 thoughts on “ C++ Program for Gauss-Elimination for solving a System of Linear Equations ” Orest March 22, 2016. Get the official BragitOff App. May 04, 2013 This page will show you how to program in C++. Gaussian elimination with pivoting. Gaussian elimination with pivoting; Gaussian elimination without.
Nonzero but very small pivot element will yield gross errors in further calculation and to guard against this and propagation of rounding errors, we introduce pivoting strategies. Definition: (Partial Pivoting). For in the Gaussian elimination process at stage k, let. The error in (3) is from seven to sixteen times larger than it is for (4), depending upon the component of the solution being considered. The results in (4) have one more significant digit than those in (3). This illustrates the positive effect that the use of pivoting can have on the error for Gaussian elimination. Scaling: It has been observed that if the elements of the coefficient matrix A vary greatly in size, then it is likely that large loss of significance errors will be introduced and the propagation of rounding errors will be worse.
To avoid this problem, we usually scale the matrix A so that the elements vary less. This is usually done by multiplying the rows and columns by suitable constants.
If we let B denote the result of row and column scaling in A, then. Therefore, if some elements of are large, a small component of r can still mean a large difference between and, or conversely, may be far from but r can nevertheless still be small. In other words, an accurate solution (i.e a small difference between and ) will always produce small residuals but small residuals do not guarantee an accurate solution. If the system is such that contains some very large elements, then we say the matrix and, therefore, the system of equations is ill-conditioned.
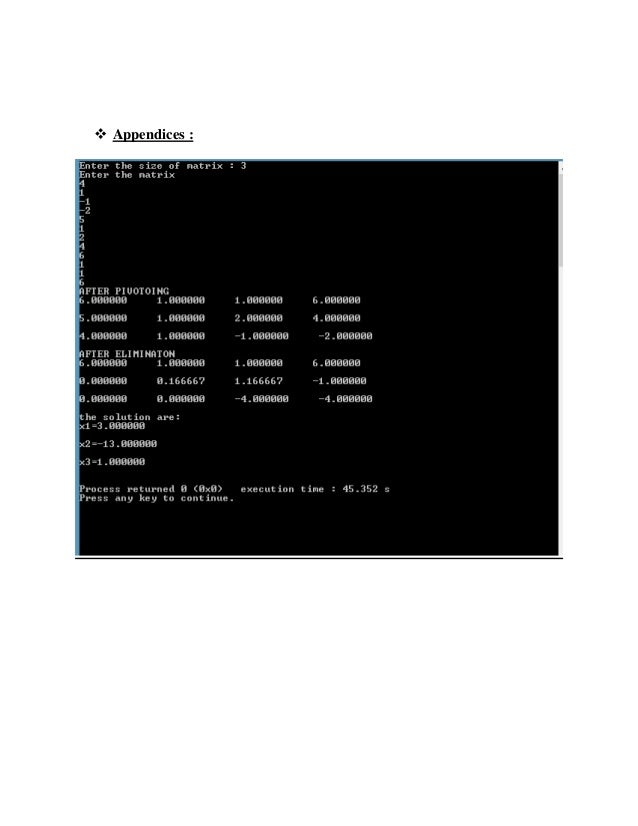
Gauss Elimination Method Example
The following simple example will illustrate the dangers inherent in solving ill-conditioned system. Consider the system. It is this error we shall try to estimate here. Any bound on E will depend on the magnitude of the round off errors incurred, the order of the matrix A, and the size of. One approach to finding such a bound would be to consider the worst possible case of round off at each stage of the method and to derive a bound based on the accumulation of these errors. Since the round off at one stage is quite complicated function of the round off at previous stages, such bounds are difficult to calculate.
Instead our approach here will be to estimate the perturbed system of equations whose true solution is the calculated solution. That is, the computed solution is the true solution of some system which we write as. Where is the error in the initial approximation.
We must now show that regardless of what the initial error is, Theorem: The iteration defined by (31) will converge for any choice of the initial vector if and only if the eigenvalues of the matrix B are all less than one in magnitude. Remark: The rate of convergence depends upon the magnitude of the largest eigen value of B. The smaller this eigen value, the faster the rate of convergence.
This theorem is not, however, very helpful in practice because we will generally not know the eigen values of B. We shall describe sufficient condition for convergence in the following Theorem, which is more practicable. Theorem: In the jacobi iteration, let the elements of B satisfy the column sum inequalities.
Gaussian elimination is designed to solve systems of linear algebraic equations, AX = This program reads input from a file which is passed as an argument when calling the program. Say the matrix is in file name matrix.txt so we call the program in this way: - gauss matrix.txt - In the matrix.txt file the inputs should be in this way: 1. First the dimension of the matrix n, this program works ONLY with square matrices. The coeffiecients of the variables of the equations 3. The constants of the equations, respectively.

C++ Program For Gauss Elimination Method
For example a sample input file would be like this - 3 3 -0.1 -0.2 0.1 7 -0.3 0.3 -0.2 10 7.85 -19.3 71.4 - Entries just need to be white-space separated. About the algorithm: This program includes modules for the three primary operations of the Gauss elimination algorithm: forward elimination, back substitution, and partial pivoting. It implements scaled partial pivoting to avoid division by zero, and during pivoting it also checks if any diagonal entry is zero, thus detecting a singular system. The equations are not scaled, but scaled values are used to determine the best partial pivoting possible.

Matrices are allocated in such a way so that the index starts from 1, not from zero. So the first element of a matrix A is A11, not A00. The co-efficient matrix must be a square one. The constant matrix has been implemented as a column. Although it could have been implemented as an n x 1 matrix, I chose not to.